Astounding Hindu units of time
No way humans could have come up with these numbers, even by imagination.
Hindu texts describe units of Kala measurements, from microseconds to Trillions of years.[1] According to these texts, time is cyclic, which repeats itself forever.[2]
Time units[
Various units of time are used across the Vedas, Bhagavata Purana, Vishnu Puran, Mahabharata, Suryasidhanta etc .
Sidereal metrics[
| Unit | Definition | Relation to SI units | |
|---|---|---|---|
| त्रुति | Base unit | ≈ 0.031 µs | |
| Renu | रेणु | 60 | ≈ 1.86 µs |
| Lava | लव | 60 Renu | ≈ 0.11 ms |
| Līkṣaka | लीक्षक | 60 Lava | ≈ 6.696 ms |
| लिप्ता | 60 Leekshaka | ≈ 0.401 s | |
| विपल | |||
| पल | 60 | ≈ 24.1056 s | |
| Vighaṭi | विघटि | ||
| Vinādī | विनाडी | ||
| Ghaṭi | घटि | 60 Vighaṭi | ≈ 24 min |
| Nādī | नाडी | ||
| दण्ड | |||
| Muhūrta | मुहूर्त | 2 Ghaṭi | ≈ 48 min |
| Nakṣatra Ahorātram (Sidereal Day) | नक्षत्र अहोरात्रम् | 60 Ghaṭī | ≈ 24 h |
| 30 Muhūrta | ≈ 24 h | ||
| Unit | Definition | Relation to SI units |
|---|---|---|
| Base unit | ≈ 35.5 µs | |
| 100 | ≈ 3.55 ms | |
| 30 Tatpara | ≈ 106.7 ms | |
| Kāṣṭhā | 30 Nimesha | ≈ 3.2 s |
| Kalā | 30 Kāṣṭhā | ≈ 1.6 min |
| Muhūrta | 30 Kalā | ≈ 48 min |
| Nakṣatra Ahorātram (Sidereal Day) | 30 Muhūrta | ≈ 24 h |
Small units of time used in the Vedas[
| Unit | Definition | Relation to SI units |
|---|---|---|
| Paramāṇu | Base unit | ≈ 26.3 µs |
| Aṇu | 2 Paramāṇu | ≈ 52.67 µs |
| Trasareṇu | 3 Aṇu | ≈ 158 µs |
| Truṭi | 3 Trasareṇu | ≈ 474 µs |
| 100 Truṭi | ≈ 47.4 ms | |
| Lava | 3 | ≈ 0.14 s |
| Nimeṣa | 3 Lava | ≈ 0.43 s |
| Kṣaṇa | 3 Nimesha | ≈ 1.28 s |
| Kāṣṭhā | 5 Kṣaṇa | ≈ 6.4 s |
| 15 Kāṣṭhā | ≈ 1.6 min | |
| 15 | ≈ 24 min | |
| Muhūrta | 2 | ≈ 48 min |
| Ahorātram (Day) | 30 Muhūrta | ≈ 24 h |
| 30 Ahorātram | ≈ 30 days | |
| Ritu (Season) | 2 | ≈ 2 months |
| Ayana | 3 Ritu | ≈ 6 months |
| 2 Ayana | ≈ 365 days[4] | |
| Ahorātram of Deva |
Lunar metrics[
- A Tithi or lunar day is defined as the time it takes for the longitudinal angle between the moon and the Sun to increase by 12°
. - A Paksa (also Pakṣa) or lunar fortnight consists of 15 tithes.[5]
- A Māsa or lunar month (approximately 29.5 days) is divided into 2 Pakṣas: the one between new moon and full moon (waxing) is called
gaura paksha - A Ṛitu (or season) is 2 Māsa[5]
- An Ayana is 3 Ṛitus[5]
- A year is
two
Tropical metrics[
- A Yāma = 1/4 of a day (light) or night
[ - Eight Yāmas make half of the day (either day or night)
- An Ahorātra is a tropical day (Note: A day is considered to begin and end at sunrise, not midnight.)[7]
| Name | Definition | Equivalence | |
|---|---|---|---|
| याम | ¼th of a day (light) or night | ≈ 3 hours | |
| Sāvana Ahorātram | सावन अहोरात्रम् | 8 Yamas | 1 Solar day |
Reckoning of time among other entities[
Among the Pitṛs (forefathers)
- 1 day of
pitras masa - 30 days of
pitras pitras - 12 months of
pitras pitras
The Lifespan of the pitras is 100 years of pitras (3,000 Solar years).[7]
Among the Devas[
The life span of any Hindu deva spans nearly (or more than) 4.5 million years. Statistically, we can also look it as :
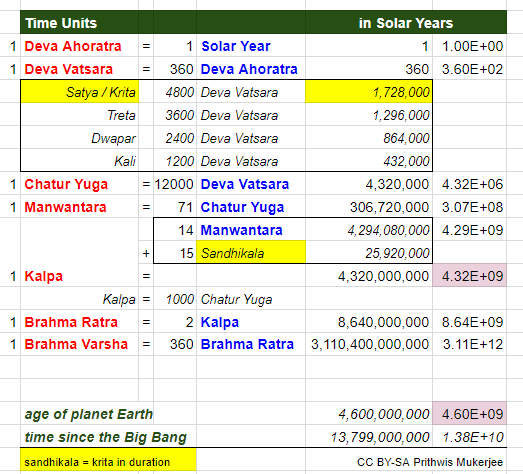
- 12000 Deva Years = Life Span of Devas = 1 Mahā-Yuga.[8]
The Viṣṇu Purāṇa Time measurement section of the Viṣṇu Purāṇa Book I Chapter III explains the above as follows:
- 2 Ayanas (6-month periods, see above) = 1 human year or 1 day of the
devas - 4,000 + 400 + 400 = 4,800 divine years (= 1,728,000 human years) = 1 Satya Yuga[8]
- 3,000 + 300 + 300 = 3,600 divine years (= 1,296,000 human years) = 1 Treta Yuga[8]
- 2,000 + 200 + 200 = 2,400 divine years (= 864,000 human years) = 1 Dvapara Yuga[8]
- 1,000 + 100 + 100 = 1,200 divine years (= 432,000 human years) = 1 Kali Yuga[8]
- 12,000 divine
year = 4 Yugas (= 4,320,000 human years) = 1 Mahā-Yuga (also is equaled to 12000 Daiva (divine) Yuga)[8] - [2*12,000 = 24,000 divine year = 12000 revolutions of
sun around its dual][8]
For Brahma[ edit]
- 1000 Mahā-Yugas = 1 Kalpa = 1 day (day only) of Brahma
(2 Kalpas constitute a day and night of Brahma, 8.64 billion human years)
- 30 days of Brahma = 1 month of Brahma (259.2 billion human years)
- 12 months of Brahma = 1 year of Brahma (3.1104 trillion human years)
- 50 years of Brahma = 1 Parārdha (156,764,160,000,000 human years)
- 2
parardhas = 100 years of Brahma = 1 Para = 1 Mahā-Kalpa (the lifespan of Brahma) (313,528,320,000,000 human years)
One day of Brahma is divided into 1000 parts called charaṇas.[9]
Four Yugas[ edit]
| 4 charaṇas (1,728,000 solar years) | Satya Yuga |
| 3 charaṇas (1,296,000 solar years) | Treta Yuga |
| 2 charaṇas (864,000 solar years) | Dvapara Yuga |
| 1 charaṇas (432,000 solar years) | Kali Yuga |
| Source: [1] | |

The cycle repeats itself, so altogether there are 1,000 cycles of Mahā-Yuga in one day of Brahma.
- One cycle of the above four Yugas is one Mahā-Yuga (4.32 million solar years)
as is confirmed by the Gītā Śloka 8.17 (statement) "sahasra-yuga-paryantam aharyad brahmaṇo viduḥ rātriṁyuga -sahasrāntāṁte 'ho-rātra-vido janāḥ", meaning, a day ofbrahma is of 1000 Mahā-Yuga. Thus a day of Brahma, Kalpa, is of duration: 4.32 billion solar years. Two Kalpas constitute a day andnight (Adhi Sandhi) of Brahma.[10]- A Manvantara consists of 71 Mahā-Yuga (306,720,000 solar years). Each Manvantara is ruled by a Manu.[11]
- After each Manvantara follows one Saṃdhi Kāla of the same duration as a Kṛta Yuga (1,728,000 = 4 Charaṇas). (It is said that during a Saṃdhi Kāla, the entire earth is submerged in water.)[11]
- A Kalpa consists of a period of 4.32 Billion solar
years followed by 14 Manvataras and Saṃdhi Kalas.[11] - A day of Brahma equals
- (14 times 71 Mahā-Yuga) + (15 × 4 Charaṇas)
- = 994 Mahā-Yuga + (15 * 4800)
- = 994 Mahā-Yuga + (72,000 years
) [deva years] / 6 = 12,000[ deva years] viz.one maha yuga . - = 994 Mahā-Yuga + 6 Mahā-Yuga
- = 1,000 Mahā-Yuga.[9]
Current Date[
Currently, 50 years of Brahma have elapsed. The last Kalpa at the end of 50th year is called Padma Kalpa. We are currently in the first 'day' of the 51st year.[12] This Brahma's day, Kalpa, is named as Shveta-Varaha Kalpa. Within this Day, six Manvantaras have already elapsed[13] and this is the seventh Manvantara, named as – Vaivasvatha Manvantara (or Sraddhadeva Manvantara). Within the Vaivasvatha Manvantara, 27 Mahayugas[13] (4 Yugas together is a Mahayuga), and the Krita,[14] Treta and Dwapara Yugas of the 28th Mahayuga have elapsed. This Kaliyuga is in the 28th Mahayuga. This Kaliyuga began in the year 3102 BCE in the proleptic Julian Calendar.[15] Since 50 years of Brahma have already elapsed, this is the second Parardha, also called as Dvithiya Parardha.
Calculating the elapsed time since current Brahma's creation[
432000 × 10 × 1000 × 2 = 8.64 billion years (2 Kalpa (day and night))
8.64 × 109 × 30 × 12 = 3.1104 Trillion Years (1 year of Brahma)
3.1104 × 1012 × 50 = 155.52 trillion years (50 years of Brahma)
3.1104 × 1012 × 50 = 155.52 trillion years (50 years of Brahma)
(6 × 71 × 4320000) + 7 × 1.728 × 10^6 = 1852416000 years elapsed in first six Manvataras, and Sandhi Kalas in the current Kalpa
27 × 4320000 = 116640000 years elapsed in first 27 Mahayugas of the current Manvantara
1.728 × 10^6 + 1.296 × 10^6 + 864000 = 3888000 years elapsed in current Mahayuga
3102 + 2017 = 5119 years elapsed in current Kaliyuga.
So the total time elapsed since current Brahma is
155520000000000 + 1852416000 + 116640000 + 3888000 + 5119 = 155,521,972,949,119 years
(one
Total age of Brahma is 100 (Brahma Years) which is equal to 313,528,320,000,000 Human years
The current Kali Yuga began at midnight 17 February / 18 February in 3102 BCE in the proleptic Julian calendar.[16] As per the information above about Yuga
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++




Similarly there was a rising need for better navigational methods including keeping accurate time on voyages of exploration and large prizes were offered to mathematicians who specialized in astronomy. Again, there were many such requests for information across the world from leading Jesuit researchers in Europe. Kerala mathematicians were hugely skilled in this area.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Manchester Univ. Confirms: This is How Isaac Newton Stole Concept of Gravity from a Hindu Gurukul
A little known school of scholars in south India discovered one of the founding principles of modern mathematics hundreds of years before Isaac Newton according to this new finding by Manchester University. Many would not believe how christian missionaries also helped in transporting this Information to Britian in 15th Century .
Dr George verghese Joseph from The University of Manchester says the ‘Kerala School’ identified the ‘infinite series’- one of the basic components of calculus – in about 1350. The discovery is currently and wrongly attributed in books to Sir Isaac Newton and Gottfried Leibnitz at the end of the seventeenth centuries.

The team from the Universities of Manchester and Exeter reveal the Kerala School also discovered what amounted to the Pi series and used it to calculate Pi correct to 9, 10 and later 17 decimal places.
And there is strong circumstantial evidence that the Indians passed on their discoveries to mathematically knowledgeable Jesuit missionaries who visited India during the fifteenth century. That knowledge, they argue, may have eventually been passed on to Newton himself.
Dr Joseph made the revelations while trawling through obscure Indian papers for a yet to be published third edition of his best selling book ‘The Crest of the Peacock: the Non-European Roots of Mathematics’ by Princeton University Press.

He said: “The beginnings of modern maths is usually seen as a European achievement but the discoveries in medieval India between the fourteenth and sixteenth centuries have been ignored or forgotten.
The brilliance of Newton’s work at the end of the seventeenth century stands undiminished – especially when it came to the algorithms of calculus. But other names from the Kerala School, notably Madhava and Nilakantha, should stand shoulder to shoulder with him as they discovered the other great component of calculus- infinite series.
There were many reasons why the contribution of the Kerala school has not been acknowledged – a prime reason is neglect of scientific ideas emanating from the Non-European world – a legacy of European colonialism and beyond. But there is also little knowledge of the medieval form of the local language of Kerala, Malayalam, in which some of most seminal texts, such as the Yuktibhasa, from much of the documentation of this remarkable mathematics is written.

He added: “For some unfathomable reasons, the standard of evidence required to claim transmission of knowledge from East to West is greater than the standard of evidence required to knowledge from West to East.
Certainly it’s hard to imagine that the West would abandon a 500-year-old tradition of importing knowledge and books from India and the Islamic world. But we’ve found evidence which goes far beyond that: for example, there was plenty of opportunity to collect the information as European Jesuits were present in the area at that time.
They were learned with a strong background in maths and were well versed in the local languages. And there was strong motivation: Pope Gregory XIII set up a committee to look into modernizing the Julian calendar.

On the committee was the German Jesuit astronomer/mathematician Clavius who repeatedly requested information on how people constructed calendars in other parts of the world. The Kerala School was undoubtedly a leading light in this area.




Nenhum comentário:
Postar um comentário